Over-Parameterization and Optimization III - From Quadratic to Deep Polynomials

The promise of projection based optimization in the canonical space leads us on a journey to generalize the shallow model to deep architectures. The journey is only partially successful, but there are some nice views along the way.

Last time, we used the canonical representation of neural networks to come up with a new optimization algorithm for shallow quadratic networks, by treating them as a symmetric quadratic form and performing low-rank projections. This algorithm is clearly beneficial theoretically, as it allowed us to easily obtain results that were difficult to develop by analyzing SGD. We also saw a hint of empirical potential, but our projection algorithm can’t be practical in reality without adapting it to functions with multiple outputs. If we succeed in generalizing the algorithm to multiple outputs, it won’t only allow us to optimize shallow multi-class classifiers, but will also allow us to embed the quadratic model as a “quadratic layer” within deep neural networks, while optimizing with projections instead of with regular SGD.

One would think that adding additional outputs shouldn’t be a big deal, but it’s not as straightforward as one would hope and requires some changes to the algorithm and model…

• A New Quadratic Model
  • Adapting the Model
  • Analyzing the New Model vs the Old
    • Computation
    • Parameter Count & Computational Complexity
    • Expressivity
    • Optimization With SGD
• The GLRAM Projection Algorithm
  • GLRAM’s Original Objective - Dimensionality Reduction
  • The Algorithm
  • But Does It Work?
• Deep Polynomial Networks
  • Stacking Layers
  • Combining Backpropagation and GLRAM Projections
  • Issues Scaling Up
• Summary
• Footnotes

A New Quadratic Model

When we had a single output, we could look at out model as a quadratic function that is canonically parameterized as a symmetric matrix $A \in \mathbb{R}^{d \times d}$. The projection step from a general $A$ to a neural network with $r$ hidden neurons was then just an eigendecomposition of $A$, where the assumption was that the rows of $W$ could be taken to be orthogonal without hurting the expressivity of the neural network¹. While this is true for a single output, the orthogonality of $W$ becomes restrictive when we have several outputs.

Having $n$ outputs for the same quadratic layer basically means that the projection step requires finding a shared $W$ for $\{A_{n}\}_{i=1}^{n}$, with every $A_{i}$ being distinct only through it’s $\alpha_{i}$ vector. Since the $W$ are shared and we aren’t guaranteed that the different $A_{i}$s share the same spectrum, constraining the $W$s to be orthogonal is restrictive and the natural projection using an eigendecomposition of the mean of the $A_{i}$s becomes sub-optimal. In other words, the following optimization problem can’t be solved analytically:

$$\underset{W,\alpha}{argmin} \sum_{i=1}^{n} || A_{i} - \sum_{r}\alpha_{i,r}w_{r}w_{r}^{T} ||_{F}^{2}$$

Adapting the Model

Clearly, the projection algorithm for the quadratic model can’t be useful in a practical sense without it being relevant for multiple output functions. This leads us to try to change the model in order to allow for projections. The first step towards having a model that allows projections, is to observe that the parameterization of our model can be rewritten in the following way:

$$A = \sum_{i=1}^{r} \alpha_{i}w_{i}w_{i}^{T} = W^{T}DW$$ $$D_{i,i} = \alpha_{i}$$

In words, we can look at $A$ not only as a sum of rank-$1$ matrices, but also as it’s matrix eigendecomposition. In this view, we know that we can’t project several matrices onto the same $W$ with different diagonal $D$ matrices, but maybe if we relax the parameterization and allow $D$ to be symmetric, we could get away with the projection…

Renaming $D$ as $S$, our parameterized model will now consist of $n$ matrices with the following parameterization:

$$A_{i} = W^{T}S_{i}W$$

Where $S_{i}$ is symmetric and $W \in \mathbb{R}^{r \times d}$. We will soon see that this extension of our model allows for a new projection-based optimization algorithm, but how does this new model compare to the original parameterization? Is it even still a neural network?

Analyzing the New Model vs the Old

Relaxing the model to allow for a symmetric matrix instead of a diagonal one changes the model, so we should first understand the differences between the two models.

Computation

The first thing we should understand with this model, is how it is computed. In the original parameterization, the fact that $D$ was diagonal allowed us to look at every row of $W$ in parallel and use the squared activation function instead of explicitly calculating $w_{i}^{T}x$ twice. This made the quadratic function look like a neural network, having a fully connected layer followed by an element-wise non-linear activation.

This efficient representation and calculation sadly goes away when we allow a symmetric $S$, since there is interaction between the rows of $W$. The function we are now trying to compute is the following:

$$A_{i} = x^{T}W^{T}S_{i}Wx$$

We can see that there is still computation that can be shared between the different matrices - all matrices have a quadratic form applied to $Wx$. This means we can calculate the $n$ functions efficiently by first applying a fully connected layer to $x$, moving from $d$ dimensions to $r$ ($h=Wx$). Then, instead of an element-wise activation, we run a quadratic form on the hidden layer for every output ($h^{T}S_{i}h$).

So, our model is a bit less “neural networky” since it has vector activations instead of element-wise activations, but it still has the property of sequential computation and efficiently representing $n$ functions with parameter sharing. This model is a bit less easy to draw in a network diagram, but here goes nothing:

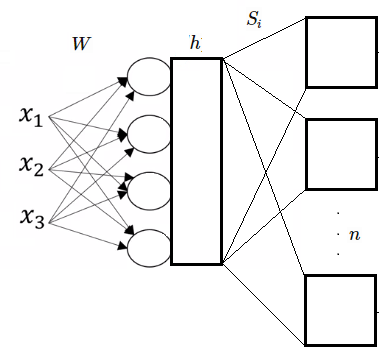
Parameter Count & Computational Complexity

Allowing $S$ to be symmetric instead of diagonal introduces more parameters to our model, so we should make a comparison between the two models to try and see when the new model is reasonable.

The original single-output model has $W \in \mathbb{R}^{r \times d}$ and $\alpha \in \mathbb{R}^{r}$, which means that overall we had $r(d+1)$ parameters. Assuming we have $n$ outputs and train the old model with regular SGD, $\alpha$ becomes a matrix and the number of parameters becomes $N_{old} = r(d+n)$. The new model has the same $W$ matrix, but this time every $S$ requires $\frac{r(r+1)}{2}$ parameters. This means that the number of parameters for the new model is $N_{new} = dr + n\frac{r(r+1)}{2}$

If we compare the two models asymptotically in parameter count, we get that $N_{old} = O(rd + rn)$ and $N_{new} = O(rd + r^{2}n)$. This means that the two models are comparable in parameter count when $r \approx \sqrt{d}$.

The computational complexity of a forward pass between the two models coincides with the number of parameters asymptotically, and the analysis is similar…

Expressivity

The final comparison we’ll run before moving to optimizing our new model, is an expressivity comparison. Namely, which model is more expressive for every $r$.

Clearly, for a given $r$ the new model is more expressive than the old model, since $S$ being symmetric still allows it to be diagonal. This means that if we define $\mathcal{H}_{diag}^{d,r,n}$ as the hypothesis class of the old model with $r$ hidden neurons and $n$ outputs and $\mathcal{H}_{sym}^{d,r,n}$ as the hypothesis class of the new model with $r$ hidden neurons and $n$ outputs, we have the containment:

$$\mathcal{H}_{diag}^{d,r,n} \subset \mathcal{H}_{sym}^{d,r,n}$$

However, can we bound the new model’s expressivity using the old model with more hidden neurons and get a two-way containment?

The answer is yes!

We can build a basis for all symmetric matrices in $\mathbb{R}^{r \times r}$, made up of rank-1 matrices. Since the space of symmetric matrices is $\frac{r(r+1)}{2}$ dimensional, we can build such a basis using $\frac{r(r+1)}{2}$ matrices. One possibility for such a basis, is the following - $\forall j \le i: (e_{i}+e_{j})(e_{i}+e_{j})^{T}$.

Now that we have such a basis, we can construct an old quadratic model with $\frac{r(r+1)}{2}$ hidden neurons in the following way:

We start with the original $W$ from a given new model and get an output of $r$ hidden neurons. Now, we add another matrix multiplication $U$ that has $\frac{r(r+1)}{2}$ outputs, each one being a basis vector. The two matrices can be multiplied to form the model’s actual $W$ matrix, which is followed by the squared activation. This construction causes the hidden layer’s activations to be the projection of $(Wx)(Wx)^{T}$ on every basis matrix. Since the basis spans the space of symmetric matrices in $\mathbb{R}^{r \times r}$, every symmetric matrix can be expressed as a linear combination of these activations and so every $S_{i}$ can be encoded using an $\alpha$ vector over the hidden outputs.

This construction is the equivalent of taking the input and raising it explicitly to the degree-2 polynomial linear space, which allows for a linear function to represent any degree-2 polynomial in that space. This construction finally gives us the two-way containment we wanted, namely:

$$\mathcal{H}_{diag}^{d,r,n} \subset \mathcal{H}_{sym}^{d,r,n} \subset \mathcal{H}_{diag}^{d,\frac{r(r+1)}{2},n}$$

We see that while the two models are different in many ways, they are still simply two ways of describing degree-2 polynomials, and so they aren’t so different. This also gives us an understanding of the difference in parameter count between the two models - if we want the old model to be as expressive as the new model, we need to make it have a similar amount of parameters overall (have $\frac{r(r+1)}{2}$ hidden neurons, leading to similar parameter count).

Optimization With SGD

The last thing to say about the new model before we start optimizing it with projections, is that this new parameterization helps us in solving one of the failures we encountered in optimizing the old model with SGD.

The old model’s element-wise activations forced every neuron’s output to sit on the rank-$1$ manifold, meaning if the optimal solution required the neuron to sit on the different side of the manifold, that neuron had to move through the origin and potentially get stuck. This new parameterization doesn’t separate the neurons anymore, and so the model isn’t restricted to be a sum of explicit rank-$1$ matrices.

Of course, the possible problem of vanishing and exploding gradients didn’t go away with this new parameterization…

The GLRAM Projection Algorithm

Now that we’ve defined our new model and convinced ourselves that it isn’t that different from the old one in terms of the expressivity and parameter count tradeoff, we can move on to deriving a projection algorithm. For that, we will look at a generalization of low-rank approximation derived originally for data in matrix form, called GLRAM (Generalized Low-Rank Approximation of Matrices).

GLRAM’s Original Objective - Dimensionality Reduction

GLRAM was originally developed as a sort of alternative to SVD, when the data we have is in matrix form. This is naturally relevant for data such as images, MRI data and other possible time-series data. For our examples and for simplification, we will assume the data is a symmetric matrix of size $n \times n$ image - $X \in \mathbb{R}^{n \times n}$.

If we wanted to run SVD/PCA in order to reduce the dimensions of the data to $r^{2} < n^{2}$, we would have to flatten every image to a vector in $\mathbb{R}^{n^{2}}$ and then find the optimal matrix $U \in \mathbb{R}^{r^{2} \times n^{2}}$ for the following optimization objective:

$$\underset{U}{argmin} \sum_{i=1}^{m}|| vec(X_{i}) - U^{T}Uvec(X_{i}) ||^{2}$$

The lower dimensional representation of $X$ is then simply $Uvec(X)$. This has two issues - first, $U$ has to be huge, causing the memory and time of the algorithm to be unnecessarily large. Second, $U$ treats the data as one-dimensional, ignoring the structure of the data.

The solution offered by GLRAM, is to treat the data in it’s matrix form and reduce it from a matrix in $\mathbb{R}^{n \times n}$ to a matrix in $\mathbb{R}^{r \times r}$. The data is reduced in dimension by a multiplication with a matrix $W \in \mathbb{R}^{d \times r}$ from both sides. The optimization objective changes to:

$$\underset{U}{argmin} \sum_{i=1}^{m}|| X_{i} - W^{T}WX_{i}W^{T}W ||_{F}^{2}$$

The lower dimensional representation of $X$ becomes $WXW^{T} \in \mathbb{R}^{r \times r}$. Note that we are able to reduce the dimension of the data to the same number of dimensions while using $rd$ parameters instead of $r^{2}d^{2}$ parameters, which is a huge savings in parameters and runtime. The GLRAM ransformation is linear like SVD, which means it is less expressive than SVD. However, because it treats the data as matrices and looks at rows and columns instead of single elements, it has a good inductive bias with respect to the data and thus performs well as a compression algorithm.

While this algorithm was originally designed for compressing data in matrix form, it is very useful for us as a projection algorithm since it’s objective is exactly the objective we have!

For a quadratic layer with $d$-dimensional input, $r$-dimensional hidden layer and $m$ outputs, we can treat the outputs as $m$ rank-$r$ matrices ${A_{i}}_{i=1}^{m}$. We are looking for a weight matrix $W \in {\mathbb{R}^{r \times d}}$ and matrices ${S_{i}\mathbb{R}^{r \times r}}_{i=1}^{m}$ such that the projection pbjective is minimized:

$$\underset{W,S}{argmin} \sum_{i=1}^{m}|| A_{i} - WS_{i}W^{T} ||_{F}^{2}$$

It turns out, that given an orthogonally-columned $W$ (not losing generality here), the optimal $S_{i}$ is $W^{T}A_{i}W$, which means we can rewrite our objective as just searching for the optimal $W$, exactly using the GLRAM objective:

$$\underset{W}{argmin} \sum_{i=1}^{m}|| A_{i} - WW^{T}A_{i}W^{T}W ||_{F}^{2}$$

Once we find $W$, we can simply set $S_{i}$ using $W$ and $A_{i}$.

The Algorithm

Sadly, while projecting with a single output was analytically solvable using an eigendecomposition or SVD, once we have multiple outputs and the new quadratic model there is no analytical solution to the projection. However, it can be solved iteratively with an alternating maximization algorithm that converges consistently to a good solution (although there are no guarantees of convergence to a global optimum).

The algorithm is detailed in depth in the paper, but I’ll quickly give the update equations here for the symmetric $A$ case. The algorithm iteratively updates $W$ by taking the top-$r$ eigenvectors of a matrix. The initial $W$ and update equations are:

$$W_{0} = eig_{r}\big( \sum_{i=1}^{m} A_{i}^{T} A_{i} \big)$$ $$W_{t} = eig_{r}\big( \sum_{i=1}^{m} A_{i}^{T}W_{t-1}^{T} W_{t-1}A_{i} \big)$$

Convergence to a fixed point can be determined by the objective function not improving by more than some $\epsilon$ after an iteration. When the $d \approx 100$, a few iterations are enough to reach convergence and 10 iterations are more than enough.

This is great - we adapted our model to have multiple outputs and allow projections from the canonical space. This means we can perform projected SGD on multiple-output functions - we simply take the current model defined by $W$ and ${S_{i}}_{i=1}^{m}$ and calculate it’s canonical representation ${A_{i}}_{i=1}^{m}$. We then take a gradient step for every $A_{i}$ using the loss function of that output and finally run GLRAM to get our new model parameterized by $\hat{W}$ and ${\hat{S}_{i}}_{i=1}^{m}$.

But Does It Work?

We went into a lot of trouble to adapt our projection algorithm to have multiple outputs, but does it actually work?

We can compare the different models and optimization methods we developed on the original MNIST problem (with the entire 10 classes). We will compare the old model trained with SGD and 25 hidden neurons, the old model trained with SGD and $\frac{25*26}{2}=325$ hidden neurons, the new model trained with SGD and hidden $25x25$ dimensional matrices and the same new model trained with GLRAM projections:

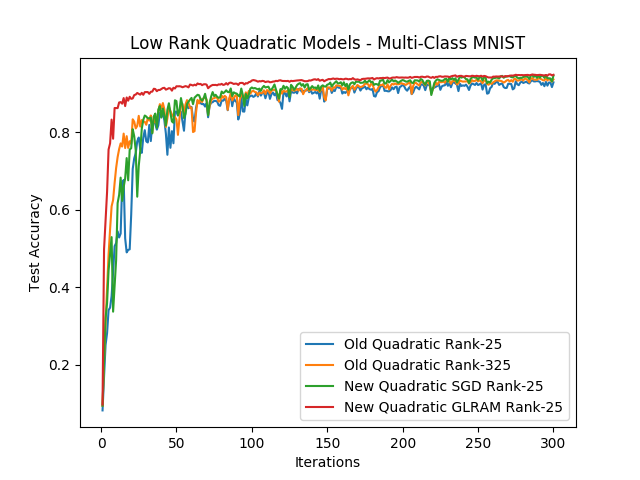
Like in the binary case with the old projection algorithm, we see an improvement in convergence with respect to regular SGD! You can find the code to this experiment here.

This is great, but we’re not done! The great thing about making a model that has multiple outputs and an optimization algorithm, is that we can now stack these models on top of each other. We can even use this model with our GLRAM optimization algorithm as a stand-alone neural network layer.

Deep Polynomial Networks

Our discussion now will be restricted to networks consisting of stacked quadratic layers forming a “deep polynomial network”. However, the concepts I’ll introduce here are more general and are relevant for any neural network for which we want to add a quadratic layer - you can have quadratic layers followed by other activation functions, pooling operators, skip connections, convolutions and whatever you want.

Stacking Layers

Notice how if we stacked two quadratic layers, feeding the output of one layer into the next, the overall model will be a degree-$2$ polynomial of degree-$2$ polynomials. This is, as you might have guessed, a degree-$4$ polynomial.

We can do this over and over again, and in every layer we add the degree of the polynomial doubles. This means that with a relativaly small number of parameters we are able to represent polynomials of degree exponential in the depth of our network. We can’t represent all high-degree polynomials of course - only those which are, informally speaking, a composition of lower degree polynomials.

You may worry that this stacking of layers only allows for a combination of monomials of degree exactly $2^{L}$, but we can bypass this problem by adding skip-connections over every quadratic layer, with a fully connected layer. This kind of model will now be able to represent polynomials with monomials up to degree $2^{L}$.

But we are faced with a big problem - the canonical space of a depth-$L$ model is no longer the space of $d \times d$ symmetric matrices - it is the space of degree-$2^{L}$ polynomials over $d$ variables. This space has $O(d^{2^{L}})$ parameters - this is super exponential in the depth of our network and is something that we clearly can’t deal with (we can neither store this many parameters nor derive a projection algorithm for such a model).

This means we’ll have to make a tradeoff - we won’t optimize in the canonical space of the entire model, but every layer will be optimized in it’s own independent canonical space…

Combining Backpropagation and GLRAM Projections

Let’s zoom in on a single quadratic layer somewhere in our deep polynomial network - the layer indexed by $t$. It has a $n_{t-1}$ dimensional inputs, $r_{t}$ hidden layer dimensions and $n_{t}$ outputs. The output of the layer before will be called $h_{t-1}(x)$, and the output of this layer will be called $h_{t}(x)$.

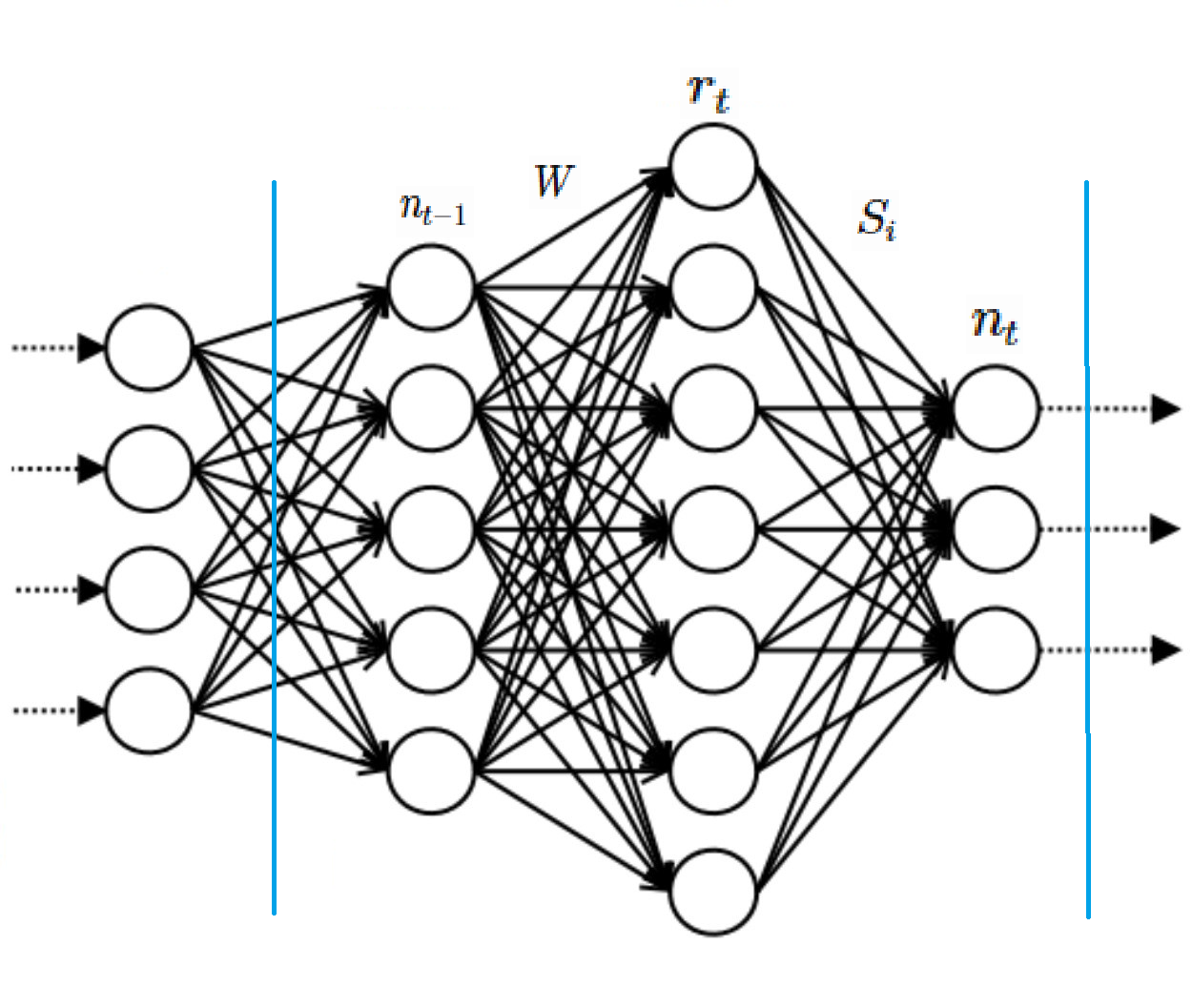
As part of the deep network, to participate in backpropegation we need to be able to compute these two things for this layer - $\frac{\partial \ell}{\partial \{ W,S \}}$ and $\frac{\partial \ell}{\partial h_{t-1}(x)}$. Luckily for us, backpropagation gives us $\frac{\partial \ell}{\partial h_{t}(x)}$ from the layer above us, so we can calculate the second gradient in the following way:

$$\frac{\partial \ell}{\partial h_{t-1}(x)} = \frac{\partial \ell}{\partial h_{t}(x)} \frac{\partial h_{t}(x)}{\partial h_{t-1}(x)}$$

This $\frac{\partial h_{t}(x)}{\partial h_{t-1}(x)}$ is a matrix with the follwing rows, which we know how to calculate using our parameters and the inputs to the layer:

$$\frac{\partial h_{t}(x)}{\partial h_{t-1}(x)}_{i,:} = \frac{\partial \big( h_{t-1}(x)^{T}A_{i}h_{t-1}(x) \big)}{\partial h_{t-1}(x)} = 2A_{i}h_{t-1}(x)$$

This is the backpropagation part, which is the same for any parameterization of our quadratic function. However, the next part is specific to our canonical representation, and that is how we calculate the gradient of the parameters:

$$\frac{\partial \ell}{\partial A} = \frac{\partial \ell}{\partial h_{t}(x)} \frac{\partial h_{t}(x)}{\partial A}$$

We already know $\frac{\partial \ell}{\partial h_{t}(x)}$ from the backpropagation from the layer above, and we can calculate $\frac{\partial h_{t}(x)}{\partial A}$ in the canonical space and then project the $A$ matrices using GLRAM!

This way, we can combine GLRAM projections to update a single layer and backpropagation to propagate the loss signal between the layers.

Issues Scaling Up

At this point, while being very promising conceptually, we run into serious problems scaling up, making this algorithm not very well suited for stacking and deep learning…

The main reason for this is the number of parameters that a single layer requires, which results in heavy time and space requirements. We can take a reasonable convolutional layer in the deeper parts of a network. Assuming we have $~100$ input dimensions and a convolutional window of size 3x3, and an output dimension of $~100$, a rank-10 quadratic layer would need $~10,000$ parameters for $W$ and another $~10,000$ parameters for the $S$ matrices.

This isn’t too bad, but in order to calculate the GLRAM projections, we need to calculate the $A$ matrices and take their gradient in the canonical space. Each of these $~100$ matrices has approximately 1 million parameters, meaning the entire layer requires storing and operating on 100 million parameters during the GLRAM projections.

While the concept of GLRAM projections is exciting, it seems that it can’t be easily applied to large models and is mostly relevant for small networks… :(

Summary

We started with an interesting premise - instead of optimizing our deep model with SGD in a parameterization which causes the loss landscape to have many critical points and weird dynamics, we can optimize in the linear canonical space and project back to the original parameterization.

Eventually, this approach led us to successful optimization algorithms which put up a fight against SGD in the original parameterization, at least when the model we’re optimizing is relatively small. However, we do see from the scaling issues that this sort of approach isn’t sustainable for deep models and less analytical activations like ReLU.

At the end of the day when we want to train very large and deep models, we can’t avoid optimizing the model in it’s annoying over-parameterized form. Still, gaining a better understanding of how the optimization behaves in this space as opposed to the canonical space can help us guide the optimization to success. It can also help us in understanding what implicit bias is introduced into our optimization process.

---

---

Footnotes

1. We needed the orthogonality assumption in order to analytically solve the projection optimization objective using an eigendecomposition. For a single symmetric $A$, this orthogonality assumption wasn’t restrictive since every symmetric matrix can be decomposed into orthogonal eigenvectors. ↩